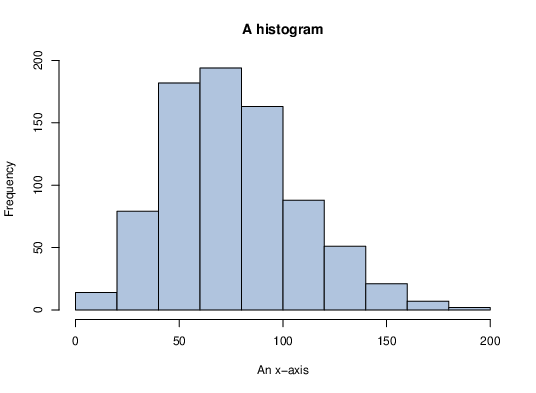
Sample Slides

Ann Example

Series Results

\begin{array}{rcl} \sum_{x = 0}^{\infty} q^{x} & = & \frac{1}{1 - q}, | q | < 1. \\ \frac{d}{d x} (\sum_{x = 0}^{\infty} q^{x}) & = & \sum_{x = 0}^{\infty} x q^{x - 1} = \sum_{x = 1}^{\infty} x q^{x - 1} = \frac{1}{(1 - q)^{2}}, | q | < 1. \\ \sum_{x = 0}^{N} q^{x} & = & \frac{1 - q^{N + 1}}{1 - q} . \\ \sum_{n = 0}^{\infty} \frac{x^{n}}{n!} & = & 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \dots = e^{x} \end{array}

Expectation

Discrete Random Variables

\begin{array}{rcl} E [g (X)] & = & \sum_{x \in S} g (x) P r (X = x) \\ V a r (X) & = & E [X^{2}] - E [X]^{2} . \end{array}

Continuous Random Variables

\begin{array}{rcl} E [g (X)] & = & \int_{- \infty}^{\infty} g (x) f_{X} (x) d x \\ V a r (X) & = & E [X^{2}] - E [X]^{2} . \end{array}

Families of Discrete Random Variables I

Bernoulli random variables, $X \sim B e r n (p)$

\begin{array}{rcl} P r (X = x) & = & {\begin{array}{cc} p, & x = 1, \\ 1 - p, & x = 0. \end{array} \end{array}

E [X] = p V a r (X) = p (1 - p) .

Binomial random variables, $X \sim B i n (n, p)$

\begin{array}{rcl} P r (X = x) & = & (\begin{array}{c} n \\ x \end{array}) p^{x} (1 - p)^{n - x}, x = 0, 1, \dots, n, \end{array}

E [X] = n p V a r (X) = n p (1 - p) .

Poisson random variables, $X \sim P o (λ), λ > 0$

\begin{array}{rcl} P r (X = x) & = & \frac{λ^{x} e^{- λ}}{x!}, x = 0, 1, 2, \dots . \end{array}

E [X] = λ V a r (X) = λ .

Families of Discrete Random Variables II

Geometric random variables, $X \sim G e o m (p)$

\begin{array}{rcl} P r (X = x) & = & p (1 - p)^{x - 1}, x = 1, 2, \dots . \end{array}

E [X] = \frac{1}{p} V a r (X) = \frac{1 - p}{p^{2}} .

Negative Binomial random variables, $X \sim N B i n (r, p)$

\begin{array}{rcl} P r (X = x) & = & (\begin{array}{cc} x - 1 \\ r - 1 \end{array}) p^{r} (1 - p)^{n - r}, x = r, r + 1, \dots . \end{array}

E [X] = \frac{r}{p} V a r (X) = \frac{r (1 - p)}{p^{2}} .

Discrete Uniform random variables, $X \sim U (1, 2, \dots, n)$

\begin{array}{rcl} P r (X = x) & = & \frac{1}{n}, x = 1, 2, \dots, n . \end{array}

E [X] = (n + 1) / 2 V a r (X) = (n^{2} - 1) / 12.

Families of Continuous Random Variables I

Uniform random variables, $X \sim U (a, b)$ ,

\begin{array}{rcl} f_{X} (x) & = & \frac{1}{b - a}, a < x < b . \end{array}

E [X] = \frac{a + b}{2} V a r (X) = \frac{(b - a)^{2}}{12} .

Exponential random variables, $X \sim E x p (λ)$ ,

\begin{array}{rcl} f_{X} (x) & = & λ e^{- λ x}, x > 0, λ > 0. \end{array}

E [X] = \frac{1}{λ} V a r (X) = \frac{1}{λ^{2}} .

Normal random variables, $X \sim N (μ, σ^{2})$ ,

f_{X} (x) = \frac{1}{\sqrt{2 π σ^{2}}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}}, - \infty < x < \infty, - \infty < μ < \infty, σ > 0.

E [X] = μ V a r (X) = σ^{2} .

Families of Continuous Random Variables II

Gamma random variables, $X \sim G a (n, λ)$ ,

f_{X} (x) = \frac{λ^{n}}{Γ (n)} x^{n - 1} e^{- λ x}, x > 0, n > 0, λ > 0, Γ (n) = (n - 1)!

E [X] = \frac{n}{λ} V a r (X) = \frac{n}{λ^{2}} .

Beta random variables, $X \sim B e t a (a, b)$ ,

\begin{array}{rcl} f_{X} (x) & = & \frac{1}{B (a, b)} x^{a - 1} (1 - x)^{b - 1} \\ = & \frac{Γ (a + b)}{Γ (a) Γ (b)} x^{a - 1} (1 - x)^{b - 1}, 0 < x < 1, a > 0, b > 0. \end{array}

E [X] = \frac{a}{a + b} V a r (X) = \frac{a b}{(a + b)^{2} (a + b + 1)} .

Column example

Here is some text in a left hand column.